PROGRAMACION LINEAL.
Un fabricante produce 2 tipos de celulares:
Jhone y Chuwei, se requiere para su elaboración dos máquinas.
Si cada máquina puede utilizarse 24 horas por día y las utilidades en los modelos Jhone y Chuwei son de 50$ y 80$, entonces….
¿Cuántos celulares de cada tipo deben elaborarse en 24 horas para obtener una utilidad máxima? ¿Cuál es la utilidad máxima?
Celular A Celular B
Jhone 2H 3H
Chuwei 4H 3H
1)PRODUCTOS:
Incógnitas
X=Jhone
Y=Chuwei
2)RESTRICCIONES:
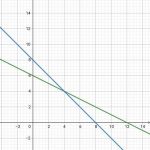
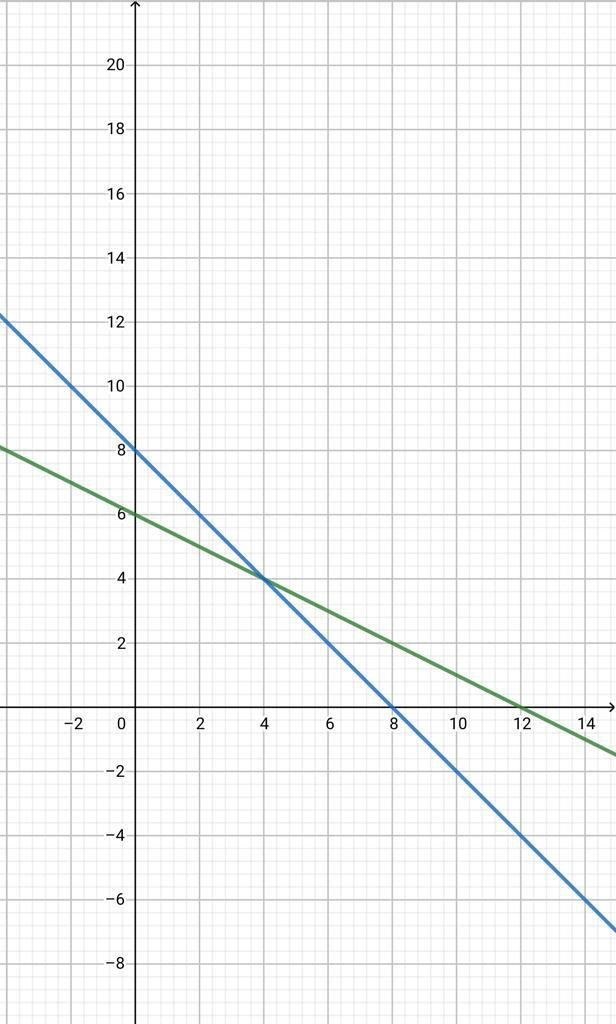
2x+4Y≤24 —> Y≤24−2𝑥/4 —> Y≤1/2X+6
3X+3Y≤24 —>Y≤24−3𝑥/3 —> Y≤-1x+8
-1/2x+6=-1x+8 Y=X+8
X – 1/2x=8-6 Y=4
1/2x= 2
x= 2*2 Y=-1/2x+6
x =4 0=-1/2x+6
X=12
3)FUNCIÓN OBJETIVO:
(X;Y)=50X+80Y
𝑃1= (0;8)→ 𝑓(𝑥)= 0.50 + 8.80= 640 → Se necesitan 0 celulares de Jhone y 8 celulares de Chuwei para obtener una utilidad máxima. La utilidad máxima es de 640.
𝑃2 = (4;4) → 𝑓(𝑥)=4.50+4.80= 520
𝑃3 = (12,0) → 𝑓(𝑥)=12.50+0.80= 600